|
Before concluding our period analysis, we need to determine how significant the signals are, and what the uncertainty (or error) is on their frequency values. Use steps 1 - 5 below to calculate the period significance, and steps 6 - 8 to determine the period error.
Determining the period significance
- Select Period significance analysis in the Period analysis menu of the last PerWin you created or click on
 in the PerWin toolbar to display the Significance analysis box. in the PerWin toolbar to display the Significance analysis box.
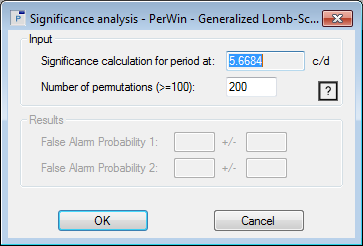
- Peranso uses a Fisher Randomization Test to calculate 2 complimentary False Alarm Probabilities (FAP) for determining the significance of a signal. Tutorial 20 explains the FAP concept in more detail.
A significance analysis requires a lot of processing power. Depending on the amount of observations in your light curve, it may take several minutes to complete.
The Significance analysis box has an Input section and a Results section. Click the OK button to calculate the significance of the signal at 5.668 c/d, using a set of 200 permutations.
- Peranso starts calculating period diagrams for each permutation.The progress of the calculations is is shown in the above box through 2 green bars. The upper bar shows the progress of calculations for one permutation, while the lower bar shows the overall progress across all 200 permutations. Intermediate FAP values and their 1-sigma error values are displayed while calculations are ongoing.

- Wait for the calculations to complete. You will find that the signal at 5.668 c/d has a very low FAP (0.0 or around 0.0) and hence a high significance. You can repeat the Significance analysis for the other Period window with the signal at 5.840 c/d. You will come to the same conclusion.
- The Cancel button is used to interrupt calculations. The Info icon
 to display a pop-up help window with some background information on the Significance calculations. to display a pop-up help window with some background information on the Significance calculations.
Determining the Period Error
- Click on the Info icon
 in the toolbar of your last PerWin to display the Info box. It shows the Time and Frequency value of the dominant period, along with an estimate of the period uncertainty (period error), indicated by the values behind the +/- symbol. We thus find that the signal at 5.6684 c/d has a period error of 0.0004. Note that because the Fisher Randomization Test involves a random component, the FAP1 and FAP2 values you see may not match the ones in our screenshot exactly. However, they should be of the same order of magnitude (0.0 or closeby). in the toolbar of your last PerWin to display the Info box. It shows the Time and Frequency value of the dominant period, along with an estimate of the period uncertainty (period error), indicated by the values behind the +/- symbol. We thus find that the signal at 5.6684 c/d has a period error of 0.0004. Note that because the Fisher Randomization Test involves a random component, the FAP1 and FAP2 values you see may not match the ones in our screenshot exactly. However, they should be of the same order of magnitude (0.0 or closeby).
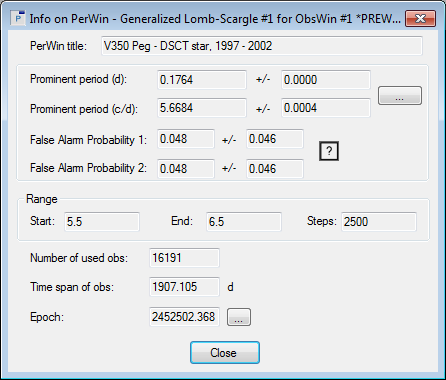
- Click on the small button labeled "...", next to the period error fields, to display the Mean Noise Power Level box. Peranso determines the minimum error of the dominant period P, by calculating a 1-sigma confidence interval on P, using a method described by Schwarzenberg-Czerny1.
That method requires the so called Mean Noise Power Level (MNPL) in the vicinity of P. Peranso calculates an approximated MNPL value, or allows the user to estimate the MNPL. The human eye appears to be a good MNPL estimator : simply look at the PerWin and estimate the mean level of the power spectrum (or equivalent) around P, ignoring all strong lines and their aliases.
Accept the default MNPL value proposed by Peranso and click OK to close the box. If you enter a different MNPL value in the Mean Noise Power Level box and click OK, then the period error values in the Info box are recalculated to reflect the new MNPL value. Use the Recalculate button to let Peranso determine the MNPL value.
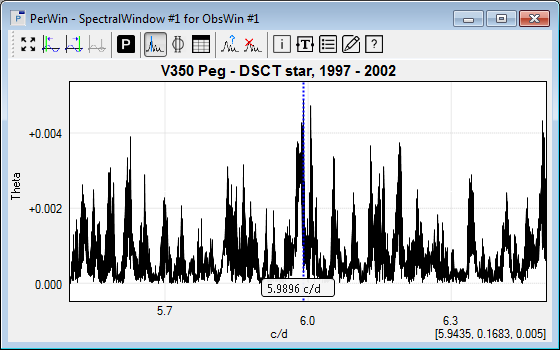
- Finally, create a Spectral Window (explained in Tutorial 2) to confirm that the periods found in the previous steps are not an artifact of the observing rate.
Conclusions
Analyzing 16191 observations of the Delta Scuti star V350 Peg, obtained between 1997 and 2002, spread over 50 sets of observations, we have ‘re-discovered’ the multi-periodic character of this variable star.
Using the Lomb-Scargle GLS period analysis method, we found a first period at 5.668 c/d and a second one at 5.840 c/d. On the basis of a Fisher Randomization method, we found very low False Alarm Probability levels, indicating that both periods are significant.
Using the Schwarzenberg-Czerny method, calculating a 1-sigma confidence interval on both periods, we found period errors of 0.0004.
(1) Schwarzenberg-Czerny, A., 1991, Mon. Not. R. astr. Soc., 253, 198-206.
|







