Period error
|
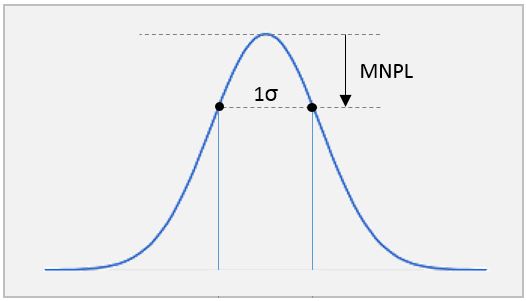
Peranso determines the minimum period error or period uncertainty of the dominant period P, by calculating a a 1-sigma confidence interval on P, using a method described by Schwarzenberg-Czerny1. This method is a so-called ‘post-mortem analysis’ and measures the width and heights of peaks/valleys in a Period Window. In his paper, Schwarzenberg-Czerny points out that most of the classical error estimation methods (some of which are present in other period analysis software) are unreliable. That’s the main reason why these methods are not supported in Peranso, despite their simplicity and speed of calculation. The period uncertainty method of Schwarzenberg-Czerny requires the so called Mean Noise Power Level (MNPL) in the vicinity of P. The 1-sigma confidence interval on P then is equal to the width of the line at the P – MNPL level.
Finding the MNPL may require some care in practice, as many low-power features appearing in a Period Window are not due to noise but are window patterns of some periods, and thus should not be taken into account. Peranso automatically calculates an approximated MNPL value to determine the period uncertainty. However, you may decide to estimate the MNPL yourself and to enter its value in the Mean Noise Power Level form. The human eye appears to be a good MNPL estimator: simply look at the Period Window and estimate the mean level of the power spectrum (or equivalent) around P, ignoring all strong lines and their aliases. Period error when using the FALC method The FALC period error value is calculated following the FALC algorithm provided by Alan Harris (JPL). It is not based on the above method of Schwarzenberg-Czerny.
|