|
We use harmonic order scans to check whether or not higher values of Orders can produce less dispersion and at which point, if any, increasing the value of Orders is no longer justified
- In the FALC Workbench select Harmonic order scan (negative increment). We know from our Regular period analysis that the dominant period is 10.319 hours. Enter this value in the Min. period (h) field. We will now instruct Peranso to hold this period constant and to try different values of Orders, starting with the number entered in the Order field and increasing by 1 for Steps number of times.The Increment field is ignored. Enter 2 in the Order field and 7 in the Steps field, then press Find.
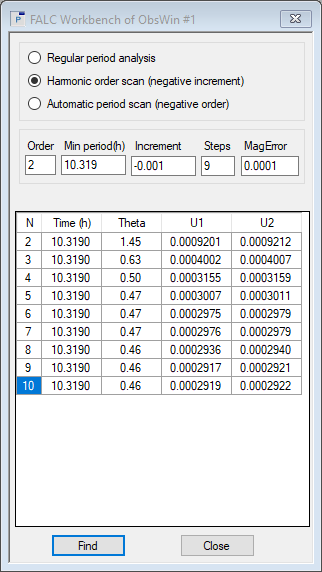
- No Period Window is displayed, but the values in the FALC Workbench table are updated. Formally, we get better Theta RMS values for higher Order values N, which might make us conclude that we have to use N = 8 (or even higher) harmonic orders. But one should be cautious here, because the Theta RMS falls under 1.0 for N > 2, that is, it is worse than the formal noise in the data.
To decide if an additional harmonic is formally significant, you can use the two columns of fit uncertainties U1 and U2 again, but this time keep in mind that each harmonic order introduces TWO new solution parameters. Therefore, the fit uncertainty has to improve by twice the difference in the two columns to be significant.
Is the 10th harmonic significant? For N = 10, we find |U1 – U2| = 0.0000003, and twice this value is 0.0000006. Between order 9 and 10, the fit uncertainty improved by 0.0002919 – 0.0002917 = 0.0000002, which is less than 0.0000006. So formally the 10th harmonic is not significant.
Is the 9th harmonic significant? For N = 9, we find |U1 – U2| = 0.0000004, and twice this value is 0.0000008. Between order 8 and 9, the fit uncertainty improved by 0.0002936 – 0.0002917 = 0.0000019, which is more than 0.0000008. So formally the 9th harmonic is significant.
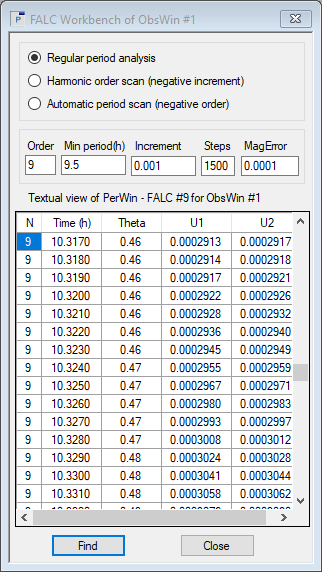
- One last refinement now is to do another period scan for N = 9, using a Regular period analysis, to really home in on the period value. We use the same period search parameters as in previous step, i.e. Min. period(h) = 9.5, Increment = 0.001, Steps = 1500, but with Order = 9. Click the Find button. We find the dominant period for 1036 Ganymed at 10.317 hours, with an uncertainty of 0.003.
|

